Bubble Sort, Insertion Sort and Selection Sort are elementary sorting algorithms, also called “quadratic”, because the time complexity of all of them is O(n2) — in the worst case. It is not actually that good, but they do excel in particular cases when the data sets are small.
Bubble Sort
In a Bubble Sort the largest values “bubble up” to the top (to the end of an array).

Here you can see how it performs in real time:
Insertion Sort
An Insertion Sort gradually creates a larger left half which is always sorted.

That is how it looks like on video:
Selection Sort
A Selection Sort places small values into sorted position.
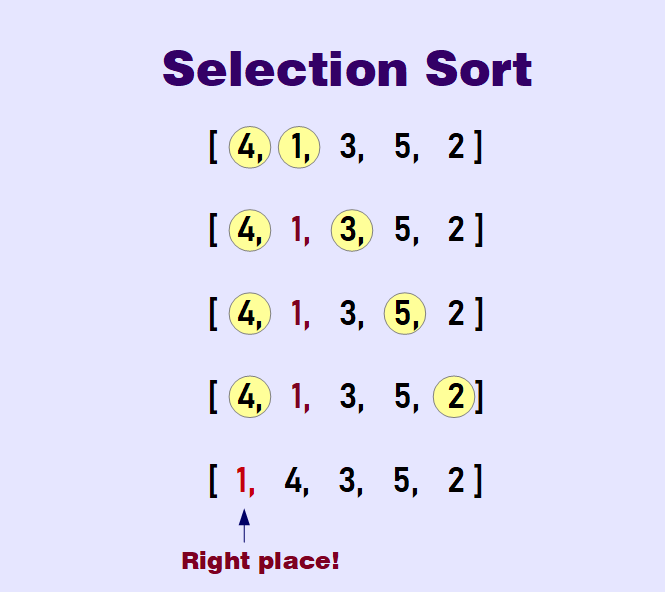
Check it out:
These three sorting algorithms are roughly equivalent, but they differ in the best cases: Bubble Sort performs very well with almost sorted data, because it has to do very little swaps. The same thing with an Insertion Sort: we iterate through the loop once doing one comparison for each item if the data is totally sorted — it's very good if you have streaming data that has to be sorted live. Selection Sort, however, doesn’t fare so well (but it’s easy to understand 😉).
As for a Space Complexity, they all perform quite well — it’s just O(1), because we’re not really using much space in these algorithms, everything is happening in place, without creating new arrays.
Merge Sort
Merge Sort decomposes an array into smaller arrays of 0 or 1 element, then it builds up a newly sorted array. As for Time Complexity, the best, the worst and the average cases are the same.

This Time Complexity is the best we can get for data-agnostic sorting algorithm (in other case we can take advantage of some weird quirk in the data). As for the Space Complexity , it’s bigger than in previous algorithms, because as we have a larger array, we have to store more arrays.
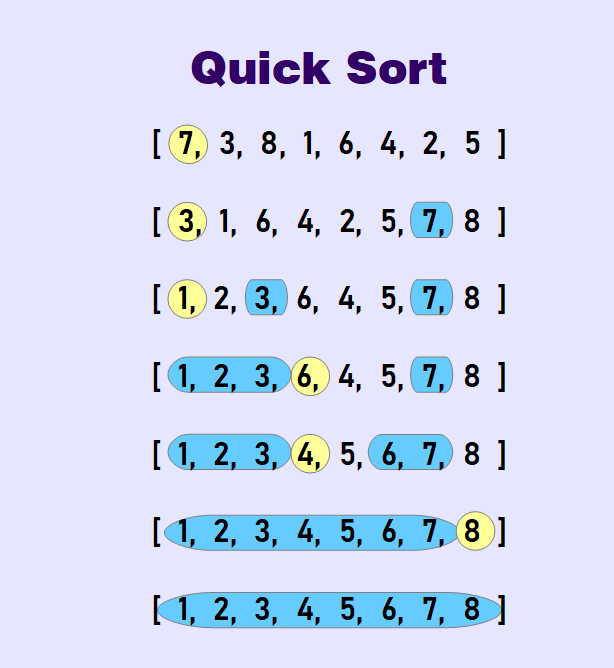
Quick Sort
Quick Sort selects one “pivot” element and finds the index where the pivot should end up. Then the algorithm can be applied on either side of the pivot.
When data is already sorted or almost sorted is the worst scenario for this algorithm. To avoid it (or at least try to avoid it) in case of sorted arrays it's better to pick pivot from the middle or any random number of the array.
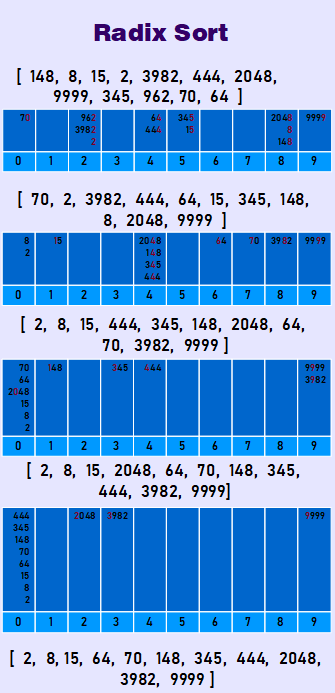
Radix Sort
Radix Sort works only on lists of numbers. It exploits the fact that information about the size of a number is encoded in the number of digits. Theoretically, it can be faster than any of the comparison sorts.
Now let's compare these Sorting Algorithms in real time!
Big O of Sorting Algorithms
| Algorithm | Time Complexity (Best) | Time Complexity (Average) | Time Complexity (Worst) | Space Complexity |
|---|---|---|---|---|
| Bubble Sort | O(n) | O(n2) | O(n2) | O(1) |
| Insertion Sort | O(n) | O(n2) | O(n2) | O(1) |
| Selection Sort | O(n2) | O(n2) | O(n2) | O(1) |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | O(n) |
| Quick Sort | O(n log n) | O(n log n) | O(n2) | O(log n) |
| Radix Sort | O(nk*) | O(nk) | O(nk) | O(n+k) |
* n - length of array, k - number of digits (average).
